Menjelajahi Dunia Bangun Datar: Contoh Soal Matematika Kelas 3 SD yang Menyenangkan dan Edukatif

Matematika seringkali dianggap sebagai mata pelajaran yang sulit bagi sebagian anak, namun sebenarnya ia adalah fondasi penting untuk memahami dunia di sekitar kita. Salah satu bab yang sangat fundamental dan dekat dengan kehidupan sehari-hari adalah Bangun Datar. Di kelas 3 SD, pengenalan dan pemahaman tentang bangun datar menjadi pijakan awal bagi konsep geometri yang lebih kompleks di jenjang selanjutnya.

Artikel ini akan membahas secara mendalam mengapa bangun datar itu penting, konsep-konsep dasar yang diajarkan di kelas 3 SD, serta menyediakan berbagai contoh soal beserta pembahasannya yang bervariasi, bertujuan untuk membantu siswa memahami materi dengan lebih baik dan menyenangkan.

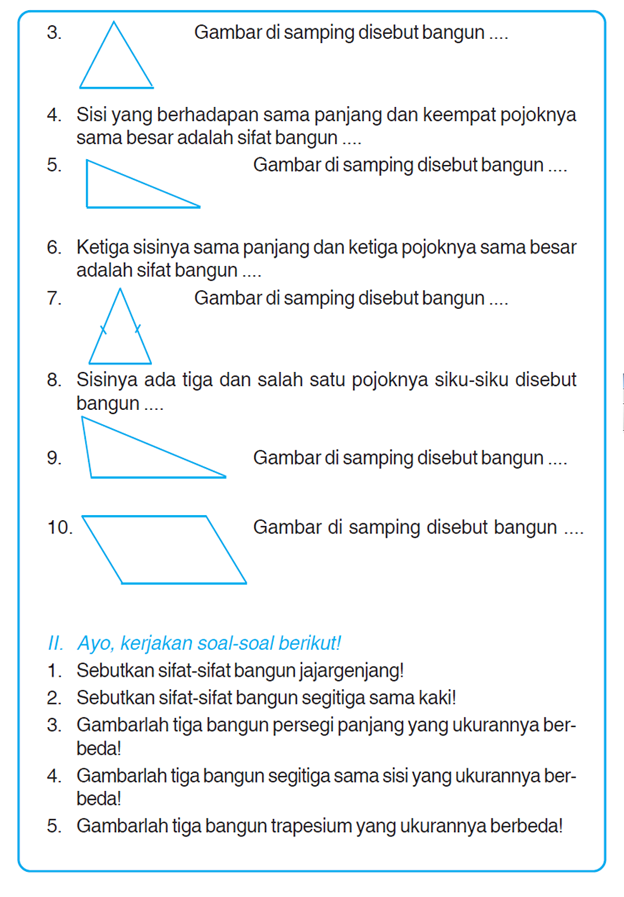
Mengapa Bangun Datar Penting untuk Kelas 3 SD?

Pemahaman tentang bangun datar bukan hanya sekadar menghafal nama-nama bentuk. Lebih dari itu, ia melatih beberapa keterampilan penting pada anak:

1. Pengamatan dan Identifikasi: Anak belajar mengenali bentuk-bentuk di lingkungan sekitar mereka, seperti jendela (persegi panjang), piring (lingkaran), atau atap rumah (segitiga).
2. Pemecahan Masalah: Soal-soal bangun datar seringkali disajikan dalam konteks kehidupan sehari-hari, melatih anak untuk menerapkan konsep matematika dalam situasi nyata.
3. Dasar Geometri: Konsep sisi, sudut, dan keliling adalah dasar yang akan terus digunakan saat mempelajari bangun ruang (3D) dan geometri analitik di tingkat yang lebih tinggi.
4. Logika dan Penalaran: Anak belajar membandingkan, mengelompokkan, dan menemukan pola dari berbagai bangun datar.
5. Kreativitas: Dengan memahami bentuk dasar, anak dapat berkreasi menggambar atau membuat objek yang kompleks dari kombinasi bangun datar.

Konsep Dasar Bangun Datar di Kelas 3 SD

Di kelas 3 SD, siswa akan dikenalkan dengan beberapa bangun datar utama dan ciri-cirinya:

1. Persegi:

   • Memiliki 4 sisi.
   • Keempat sisinya sama panjang.
   • Memiliki 4 titik sudut.
   • Keempat sudutnya berbentuk siku-siku (90 derajat).
   • Contoh: Ubin lantai, papan catur.

2. Persegi Panjang:

   • Memiliki 4 sisi.
   • Sisi yang berhadapan sama panjang.
   • Memiliki 4 titik sudut.
   • Keempat sudutnya berbentuk siku-siku (90 derajat).
   • Contoh: Pintu, buku, papan tulis.

3. Segitiga:

   • Memiliki 3 sisi.
   • Memiliki 3 titik sudut.
   • Bentuknya bisa bermacam-macam (sama sisi, sama kaki, siku-siku, sembarang).
   • Contoh: Potongan pizza, atap rumah.

4. Lingkaran:

   • Memiliki 1 sisi lengkung yang tidak memiliki titik sudut.
   • Semua titik pada lingkaran memiliki jarak yang sama dari titik pusat.
   • Contoh: Roda, koin, jam dinding.

Selain itu, siswa juga akan mulai dikenalkan dengan konsep Keliling Bangun Datar, yaitu jumlah total panjang semua sisi yang mengelilingi sebuah bangun datar. Konsep ini diajarkan secara sederhana, biasanya dengan menghitung satuan panjang pada kotak-kotak atau menjumlahkan langsung panjang sisi yang diketahui.

Contoh Soal dan Pembahasan Bangun Datar Kelas 3 SD

Berikut adalah berbagai contoh soal yang dapat digunakan untuk melatih pemahaman siswa kelas 3 SD tentang bangun datar, beserta pembahasannya yang detail.

Kategori 1: Identifikasi dan Ciri-ciri Bangun Datar

Soal 1.1: Identifikasi Bangun Datar
Perhatikan gambar-gambar bangun datar di bawah ini, lalu sebutkan nama masing-masing bangun!
A. [Gambar Persegi]
B. [Gambar Segitiga]
C. [Gambar Lingkaran]
D. [Gambar Persegi Panjang]

Pembahasan:

• A. Bangun ini memiliki empat sisi yang sama panjang dan empat sudut siku-siku. Ini adalah Persegi.
• B. Bangun ini memiliki tiga sisi dan tiga titik sudut. Ini adalah Segitiga.
• C. Bangun ini tidak memiliki sisi lurus atau titik sudut, bentuknya melingkar. Ini adalah Lingkaran.
• D. Bangun ini memiliki empat sisi, dengan sisi yang berhadapan sama panjang, dan empat sudut siku-siku. Ini adalah Persegi Panjang.

Soal 1.2: Menghitung Sisi dan Titik Sudut
Lengkapilah tabel berikut berdasarkan gambar bangun datar yang diberikan!

Gambar Bangun Datar	Nama Bangun Datar	Jumlah Sisi	Jumlah Titik Sudut
[Gambar Persegi]	Persegi	…	…
[Gambar Segitiga]	Segitiga	…	…
[Gambar Lingkaran]	Lingkaran	…	…
[Gambar Persegi Panjang]	Persegi Panjang	…	…

Pembahasan:

Gambar Bangun Datar	Nama Bangun Datar	Jumlah Sisi	Jumlah Titik Sudut
[Gambar Persegi]	Persegi	4	4
[Gambar Segitiga]	Segitiga	3	3
[Gambar Lingkaran]	Lingkaran	1 (lengkung)	0
[Gambar Persegi Panjang]	Persegi Panjang	4	4

Penjelasan: Lingkaran hanya memiliki satu sisi yang melengkung dan tidak memiliki titik sudut, karena titik sudut adalah pertemuan dari dua sisi lurus.

Soal 1.3: Ciri-ciri Bangun Datar
Manakah pernyataan yang benar tentang bangun datar Segitiga?
a. Memiliki empat sisi sama panjang.
b. Memiliki tiga titik sudut.
c. Tidak memiliki sisi lurus.
d. Semua sisinya saling berhadapan.

Pembahasan:

• a. Pernyataan ini salah. Bangun yang memiliki empat sisi sama panjang adalah persegi.
• b. Pernyataan ini benar. Segitiga selalu memiliki tiga titik sudut sebagai tempat bertemunya sisi-sisi.
• c. Pernyataan ini salah. Segitiga memiliki tiga sisi yang lurus. Bangun yang tidak memiliki sisi lurus adalah lingkaran.
• d. Pernyataan ini salah. Sisi-sisi pada segitiga tidak selalu saling berhadapan dalam artian seperti persegi atau persegi panjang.

Jadi, jawaban yang benar adalah b.

Kategori 2: Keliling Bangun Datar Sederhana

Soal 2.1: Menghitung Keliling Persegi (dengan satuan kotak)
Perhatikan gambar persegi di bawah ini yang dibentuk dari kotak-kotak satuan. Setiap sisi kotak mewakili 1 satuan panjang. Berapakah keliling persegi tersebut?
[Gambar Persegi 3×3 kotak]

Pembahasan:

• Pertama, hitung panjang satu sisi persegi. Dari gambar, satu sisi persegi terdiri dari 3 kotak satuan. Jadi, panjang sisi = 3 satuan.
• Keliling persegi adalah jumlah panjang semua sisinya. Karena persegi memiliki 4 sisi yang sama panjang, maka:
  Keliling = Sisi + Sisi + Sisi + Sisi
  Keliling = 3 satuan + 3 satuan + 3 satuan + 3 satuan
  Keliling = 12 satuan
• Atau bisa juga menggunakan rumus: Keliling = 4 x Sisi = 4 x 3 = 12 satuan.

Jadi, keliling persegi tersebut adalah 12 satuan panjang.

Soal 2.2: Menghitung Keliling Persegi Panjang (dengan ukuran diketahui)
Sebuah meja berbentuk persegi panjang memiliki panjang 5 meter dan lebar 3 meter. Berapakah keliling meja tersebut?

Pembahasan:

• Meja berbentuk persegi panjang.
• Panjang (p) = 5 meter
• Lebar (l) = 3 meter
• Keliling persegi panjang adalah jumlah panjang semua sisinya. Karena persegi panjang memiliki 2 sisi panjang dan 2 sisi lebar, maka:
  Keliling = Panjang + Lebar + Panjang + Lebar
  Keliling = 5 m + 3 m + 5 m + 3 m
  Keliling = 16 meter
• Atau bisa juga menggunakan rumus: Keliling = 2 x (Panjang + Lebar) = 2 x (5 + 3) = 2 x 8 = 16 meter.

Jadi, keliling meja tersebut adalah 16 meter.

Soal 2.3: Menghitung Keliling Segitiga (dengan ukuran diketahui)
Sebuah rambu lalu lintas berbentuk segitiga memiliki panjang sisi-sisi sebagai berikut: sisi pertama 40 cm, sisi kedua 40 cm, dan sisi ketiga 30 cm. Berapakah keliling rambu lalu lintas tersebut?

Pembahasan:

• Rambu lalu lintas berbentuk segitiga.
• Sisi 1 = 40 cm
• Sisi 2 = 40 cm
• Sisi 3 = 30 cm
• Keliling segitiga adalah jumlah panjang semua sisinya:
  Keliling = Sisi 1 + Sisi 2 + Sisi 3
  Keliling = 40 cm + 40 cm + 30 cm
  Keliling = 110 cm

Jadi, keliling rambu lalu lintas tersebut adalah 110 cm.

Soal 2.4: Soal Cerita Keliling
Lani ingin menghias sekeliling pigura fotonya yang berbentuk persegi. Jika satu sisi pigura tersebut panjangnya 20 cm, berapa panjang pita yang dibutuhkan Lani untuk menghias seluruh pigura?

Pembahasan:

• Pigura berbentuk persegi.
• Panjang satu sisi = 20 cm.
• Untuk menghias sekeliling pigura, Lani membutuhkan pita sepanjang keliling pigura.
• Keliling persegi = Sisi + Sisi + Sisi + Sisi
  Keliling = 20 cm + 20 cm + 20 cm + 20 cm
  Keliling = 80 cm
• Atau Keliling = 4 x Sisi = 4 x 20 cm = 80 cm.

Jadi, panjang pita yang dibutuhkan Lani adalah 80 cm.

Kategori 3: Pengelompokan dan Pola Bangun Datar

Soal 3.1: Mengelompokkan Bangun Datar
Kelompokkan bangun-bangun datar di bawah ini berdasarkan jumlah sisinya!
[Gambar: Segitiga, Persegi, Lingkaran, Persegi Panjang, Segitiga, Lingkaran]

Pembahasan:

• Bangun dengan 3 sisi: Segitiga, Segitiga
• Bangun dengan 4 sisi: Persegi, Persegi Panjang
• Bangun dengan 1 sisi lengkung: Lingkaran, Lingkaran

Soal 3.2: Melanjutkan Pola Bangun Datar
Perhatikan pola bangun datar berikut ini:
Persegi, Segitiga, Lingkaran, Persegi, Segitiga, …, …

Bangun datar apakah yang seharusnya mengisi titik-titik tersebut?

Pembahasan:
Pola yang terbentuk adalah pengulangan dari "Persegi, Segitiga, Lingkaran".
Setelah "Persegi, Segitiga", maka bangun selanjutnya dalam pola adalah "Lingkaran".
Setelah "Lingkaran", pola akan kembali ke awal, yaitu "Persegi".

Jadi, bangun datar yang seharusnya mengisi titik-titik adalah Lingkaran, Persegi.

Kategori 4: Aplikasi dalam Kehidupan Sehari-hari

Soal 4.1: Mengenali Bentuk di Sekitar
Sebutkan 3 benda di rumahmu yang berbentuk:
a. Lingkaran
b. Persegi panjang
c. Segitiga

Pembahasan:
Ini adalah soal terbuka, jawaban bisa bervariasi. Contoh jawaban:
a. Lingkaran: Jam dinding, piring, koin, roda sepeda, tutup toples.
b. Persegi panjang: Pintu, buku, lemari, televisi, karpet.
c. Segitiga: Gantungan baju, atap rumah (jika terlihat dari depan), potongan semangka, bendera segitiga.

Soal 4.2: Menggambar dengan Bangun Datar
Gambarlah sebuah rumah sederhana menggunakan kombinasi bangun datar persegi, persegi panjang, dan segitiga!

Pembahasan:

• Badan rumah: Dapat digambar menggunakan bangun persegi atau persegi panjang.
• Atap rumah: Dapat digambar menggunakan bangun segitiga yang diletakkan di atas badan rumah.
• Pintu dan jendela: Dapat digambar menggunakan bangun persegi panjang atau persegi kecil.

(Siswa akan menggambar. Penjelasan ini membantu memvisualisasikan).

Kategori 5: Berpikir Kritis (Sedikit Lebih Kompleks)

Soal 5.1: Membandingkan Keliling
Ada dua kebun. Kebun A berbentuk persegi dengan panjang sisi 6 meter. Kebun B berbentuk persegi panjang dengan panjang 7 meter dan lebar 5 meter. Kebun manakah yang memiliki keliling lebih besar?

Pembahasan:

• Hitung keliling Kebun A (persegi):
  Keliling Kebun A = 4 x Sisi
  Keliling Kebun A = 4 x 6 meter
  Keliling Kebun A = 24 meter

• Hitung keliling Kebun B (persegi panjang):
  Keliling Kebun B = 2 x (Panjang + Lebar)
  Keliling Kebun B = 2 x (7 meter + 5 meter)
  Keliling Kebun B = 2 x 12 meter
  Keliling Kebun B = 24 meter

• Bandingkan:
  Keliling Kebun A = 24 meter
  Keliling Kebun B = 24 meter

Ternyata, kedua kebun memiliki keliling yang sama besar, yaitu 24 meter.

Soal 5.2: Menentukan Sisi dari Keliling (untuk persegi)
Sebuah taplak meja berbentuk persegi memiliki keliling 100 cm. Berapakah panjang satu sisi taplak meja tersebut?

Pembahasan:

• Taplak meja berbentuk persegi.
• Keliling persegi = 100 cm.
• Kita tahu bahwa rumus keliling persegi adalah: Keliling = 4 x Sisi.
• Jika Keliling = 100 cm, maka:
  100 cm = 4 x Sisi
• Untuk mencari panjang satu sisi, kita perlu membagi keliling dengan 4:
  Sisi = 100 cm : 4
  Sisi = 25 cm

Jadi, panjang satu sisi taplak meja tersebut adalah 25 cm.

Soal 5.3: Kombinasi Bangun Datar
Sebuah robot mainan memiliki kepala berbentuk lingkaran, badan berbentuk persegi, dan tangan serta kaki masing-masing berbentuk persegi panjang. Berapa total bangun datar yang digunakan untuk membuat robot tersebut? Sebutkan masing-masing jenisnya.

Pembahasan:

• Kepala: 1 Lingkaran
• Badan: 1 Persegi
• Tangan: 2 Persegi Panjang (karena ada dua tangan)
• Kaki: 2 Persegi Panjang (karena ada dua kaki)

Total bangun datar = 1 (lingkaran) + 1 (persegi) + 2 (persegi panjang) + 2 (persegi panjang) = 6 bangun datar.
Jenisnya: 1 Lingkaran, 1 Persegi, dan 4 Persegi Panjang.

Tips untuk Orang Tua dan Guru dalam Mengajarkan Bangun Datar

1. Gunakan Media Konkret: Ajak anak mengidentifikasi bangun datar pada benda-benda di sekitar rumah atau sekolah (misalnya, meja, buku, jendela, piring, jam). Gunakan kertas lipat, stik es krim, atau plastisin untuk membuat berbagai bangun datar.
2. Belajar Sambil Bermain: Buat permainan tebak bentuk, susun puzzle bangun datar, atau minta anak membuat gambar dari kombinasi bangun datar.
3. Visualisasi: Gunakan gambar yang jelas dan berwarna. Ajak anak menggambar bangun datar sendiri.
4. Kaitkan dengan Kehidupan Sehari-hari: Selalu berikan contoh soal cerita yang relevan agar anak melihat manfaat belajar bangun datar.
5. Kesabaran dan Pujian: Setiap anak memiliki kecepatan belajar yang berbeda. Berikan dukungan dan pujian untuk setiap usaha dan kemajuan yang ditunjukkan anak. Jangan ragu untuk mengulang materi jika diperlukan.
6. Fokus pada Konsep, Bukan Hanya Hafalan: Pastikan anak memahami mengapa sebuah bangun disebut persegi, bukan hanya menghafal namanya.

Kesimpulan

Mempelajari bangun datar di kelas 3 SD adalah langkah awal yang sangat penting dalam perjalanan belajar matematika seorang anak. Dengan berbagai contoh soal yang bervariasi, mulai dari identifikasi sederhana hingga aplikasi keliling dan soal cerita, diharapkan siswa dapat membangun pemahaman yang kuat dan fondasi yang kokoh dalam geometri. Pendekatan yang menyenangkan, konkret, dan relevan dengan kehidupan sehari-hari akan membuat matematika menjadi petualangan yang menarik, bukan lagi sebuah momok yang menakutkan. Mari ajak anak-anak kita menjelajahi dunia bentuk dan angka dengan penuh semangat!